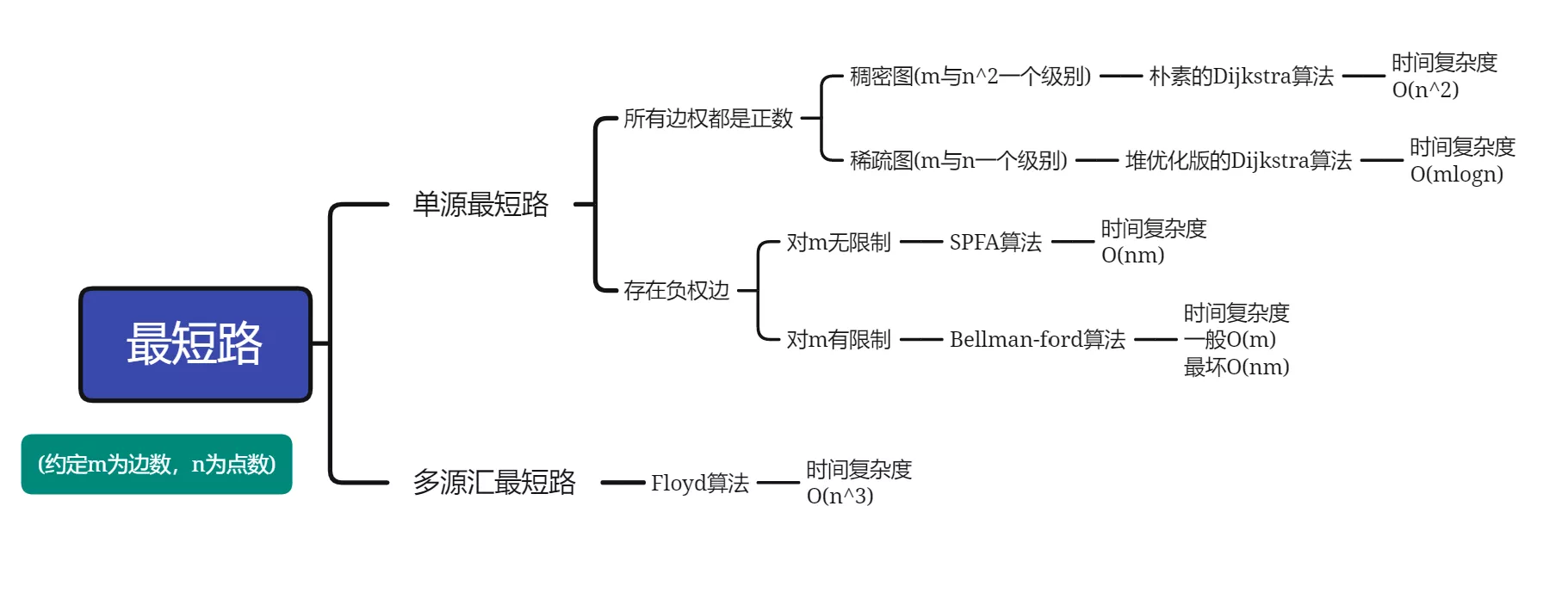
最短路
1 | Dijkstra-朴素 O(n2) |
单源最短路
点击查看
所有边权都是正数
朴素的Dijkstra算法
点击查看
1.时间复杂度O(n^2) n为点的数量
所以与堆优化版进行对比,如果边的数量m与n^2是一个级别,那就是稠密图,建议使用朴素dijkstra算法, 同时稠密图用邻接矩阵来存
2.算法实现
1 | s[]:存储所有已经确定最短距离的点 |
例题:
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。 |
1 |
|
堆优化版的Dijkstra算法
点击查看
1.时间复杂度O(mlogn) m为边的数量
与朴素算法对比,如果是稀疏图,也就是边的数量m与n是一个级别,建议使用堆优化版的dijkstra算法, 同时稀疏图用邻接表来存
2.算法实现
1 | s[]:存储所有已经确定最短距离的点 |
例题:
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。 |
1 |
|
存在负权边
Bellman-Ford算法
点击查看
1.时间复杂度 O(mn) 也就是点数乘边数
2.基本思路
1 | for(n次){ |
3.bellman-fold算法迭代的次数有实际意义
迭代k次求得的dist数组的含义是从一号点经过不超过k条边走到每个点的最短距离,所以当题目要求对经过的边数有限制的时候,要用bellman-fold算法
4.bellman-fold算法可以用来求是否存在负环
例题:
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。 |
1 |
|
SPFA算法(是Bellman-Ford的优化)
点击查看
1.时间复杂度 一般情况:O(m) 最坏:O(nm)
2.尽管是BF算法的优化,但是不是所有情况都可以使用SPFA算法
如果对经过的边数进行限制,那就只能使用Bellman-Ford算法
99%的情况都可以用spfa(不能有负环)
3.基本思路
1 | 主要思路:只用更新过的点来更新其他点 |
例题1:spfa求最短路
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。 |
1 |
|
例题2:spfa判断负环
原理:dist[x]数组的含义是当前从一号点到x点最短路径的长度,每次更新dist数组的同时更新cnt数组,表示当前最短路的边数,如果某一次cnt[x] >= n的话,由抽屉原理,经过了n条边,说明一共经过了n + 1个点,说明有点不止经过了一次,说明存在环,并且是负权环。
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。 |
1 |
|
多源汇最短路
点击查看
Floyd算法
点击查看
1.时间复杂度 O(n^3)
2.基本思路:
1 | d[i,j]邻接矩阵存储所有的边,然后三重循环 |
例题:
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。 |
1 |
|
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 adomais's blog!
评论




